Difference between revisions of "Cosmology"
| (4 intermediate revisions by the same user not shown) | |||
| Line 24: | Line 24: | ||
An iron universe... | An iron universe... | ||
| + | |||
| + | == Parenago's Discontinuity == | ||
| + | |||
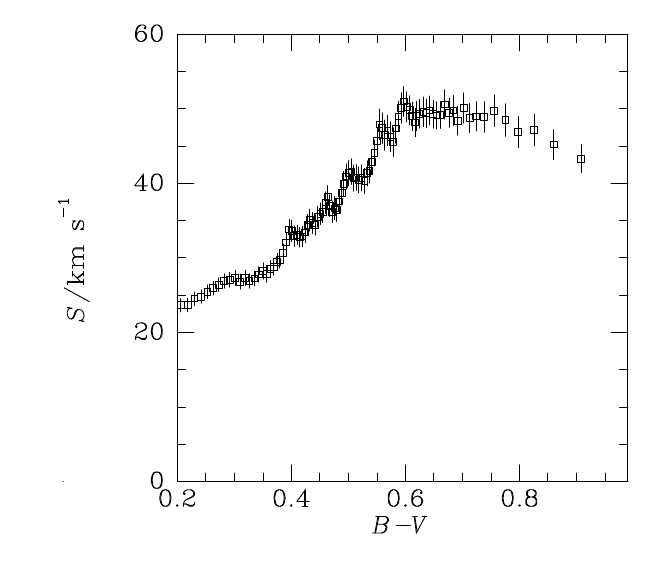
| + | [[File:parenago-discontinuity.png|thumb|Parenago's Discontinuity in a plot of stellar velocity dispersion by colour (spectral class).]] | ||
| + | Measurements of the velocity dispersion of stars (standard deviation of the relative velocity distribution) over the [https://en.wikipedia.org/wiki/UBV_photometric_system colour] (spectral class) show an inverse relationship, i.e. an increase in velocity dispersion as the surface temperature decreases, but the trend shows a discontinuity at around B-V = 0.6 (around class K5 or so), where blue-wards the velocities are more uniform, and more dispersed red-wards. This is usually interpreted in terms of stellar lifetimes being longer or shorter than τ<sub>max</sub>, the age of the stellar neighbourhood. | ||
Latest revision as of 21:57, 6 May 2019
Heim Theory
Can General Relativity be generalised upwards to more dimensions, and if so, what if anything does doing so tell us? String Theory tries 11 dimensions and disappears up its own zero point energy. The Standard Model has infinities that require arbitrary rationalisations. KK Theory tries 5 dimensions (adding mass as a fifth axis) and reduces to both Relativity and Maxwell's equations, depending on which bits you are ignoring, but the theory that has many physicists running for cover is Heim theory.
Heim theory, later developed by his colleagues, has 8 dimensions, discrete space divided into Planck lengths, selector calculus, difference operators (discrete analogs to differentials), employs conic octonions, and so on. You need serious post-graduate calculus-fu just to sweep up the lab in the morning to get started.
Once you're in, we encounter an intriguing set of calculations. They begin with only four physical constants - h, ε0, G and c, and produce the masses of the subatomic particles with incredible accuracy. Except the Higgs boson of course, which doesn't exist yet.
Iron Sun Hypothesis
One of the prevailing mysteries in solar physics is why, given the amount of H fusion in the core that is required to generate the heat and light observed at the surface, the predicted amount of neutrino flux is simply not observed, even taking into account νe - νμ conversion and coronal 3He filament absorbtion. The inner solar system should be awash with solar neutrino flux, yet the observed flux is more or less the same in any direction, and much less than standard solar theory predicts.
There is still currently no way (without resorting to peculiar or even entirely speculative physics) to explain a solar surface temperature of a relatively cool 6000 Kelvin, presumably heated from fusion within the sun, whilst the corona reaches temperatures of several million K sufficient to fuse elements and generate X-Ray spectra. See White et al. "Radio and Hard X–ray Images of High–Energy Electrons in an X-class Solar Flare".
Could H and He fusion in coronal plasma filaments, heated to millions of Kelvin by magnetohydrodynamic compression (the so-called Z-pinch), be sufficient to explain the observed solar heat budget and particle flux? And if so, what of the core of the sun?
Implications for stellar evolution
Element formation in the big picture. Big Bang nucleosynthesis. fusion to iron.
Instead of the universe consisting almost entirely of H and He, could it in fact be mostly Fe by mass?
Galaxy rotation curves; c.f. Peratt's plasma universe paper.
An iron universe...
Parenago's Discontinuity
Measurements of the velocity dispersion of stars (standard deviation of the relative velocity distribution) over the colour (spectral class) show an inverse relationship, i.e. an increase in velocity dispersion as the surface temperature decreases, but the trend shows a discontinuity at around B-V = 0.6 (around class K5 or so), where blue-wards the velocities are more uniform, and more dispersed red-wards. This is usually interpreted in terms of stellar lifetimes being longer or shorter than τmax, the age of the stellar neighbourhood.